Logic 3

It is easy to get confused about whether we are talking directly about the real world, or whether we are trying to evaluate statements about the world as to whether they have been found to be false or not, and then asking that given some sentences (often people say "some statement"), what can we conclude on that basis.

One of the things that can get confusing about negative sentences is just what is being negated. In working on a problem with logic, we are concerned only with propositions (sentences). Often, in English at least, when we negate a word inside a sentence we imply that we really mean the opposite of the word we negate. If we say, "Paul is not an Einstein," we probably mean that Paul is stupid. This may be a peculiarity of English, but I think it is a common phenomenon in other languages too. If we take words at their face value, then saying, "Yao Ming is not short," we would think that the meaning would be satisfied if Mr. Yao were over five feet tall (or whatever your threshold for shortness is). But most people would have the intention of communicating the idea that Mr. Yao is very tall. The opposite of short is tall, so saying that he is not short sounds like saying that he is tall. This kind of complication can produce misunderstandings if one person  who  is a very literal-minded speaker says, "I do not like you," and the other person assumes this means the same as, "I dislike you," or even something like, "I hate you."

When someone says, "James is not tall," it may mean that, "James is (not-tall =) short? or it may mean that, "It would be wrong to say that James is tall," or "It is not the case that James is tall."

There is always a danger in ordinary discussions of leaving out the range of possibilities between, e.g., "Today is hot!" and "Today is cold!" Keep that in mind for general references.

There are several symbols used for negating propositions (sentences) when doing formal logic. Because there is now an explicit symbol on our keyboard we will use the symbol logical not symbo;l along with parentheses to write things such as: ¬(The sky looks yellow most days.) So if we were going to use  Y to represent the sentence, "The sky looks yellow most days," we would symbolize the claim that that sentence is wrong by writing "¬Y." (Some browsers cannot handle the logical not symbol "¬". and may put "~" or some other substitute in its place. )


If we say of an untrue statement, "That statement is untrue," then our second sentence is true.

Which of the following statements are true and which are false?

¬(The sky is red.)  (T) (F)
¬(The north pole is found within the Arctic Circle.)  (T) (F)
¬(The south pole is not found somewhere on Antarctica.) (T) (F)
¬(China is in Europe.) (T) (F)
¬(Beijing is in China.) (T) (F)

Let's see what the interior truth values are:
"The sky is red," is (F) or false.
"The north pole is found within the Arctic Circle," is (T) or true.
"The south pole is not found somewhere on Antarctica,"   is (F) or false   .
"China is in Europe,"  is (F) or false.                    
"Beijing is in China," is (T) or true.
In short, that is
F
T
F
F
T

I believe the person is correct who says, "It is not the case that the sky is red." So I would mark : ¬(The sky is red.)  as (T) or true.
I believe the person is incorrect who says, "It is not the case that the north pole is found within the Arctic Circle." So  I would mark ¬(The north pole is found within the Arctic Circle.)  as (F) or false
I believe the person is correct who says, "It is not the case that the south pole is not found somewhere in Antarctica." So I would mark ¬(The south pole is not found somewhere on Antarctica.) as (T)  or true.
I believe the person is correct who says, "It is not the case that China is in Europe." So I would mark ¬(China is in Europe.) as (T)  or true.
I believe the person is incorrect who says, "It is not the case the Beijing is in China." So I would mark ¬(Beijing is in China.) (as (F) of false.
In short that is:

T
F
T
T
F


Now what would happen if some person who likes to create controversy would say that the rest of the people were all wrong. Symbolically that person would claim the negation of all the above five values:
¬ F
¬ T
¬ F
¬ F
¬ T
So if not false is true and not true is false, the
truth values of the above five sentences are:
T
F
T
T
F
The contrary or controversy-seeking person would say, "It's true that the sky is red. It's false that North Pole is found above the Arctic Circle," and so forth. You would think that nobody would believe this person, and you are probably right,  but in this lesson we are just experimenting with putting ¬ before a sentence and trying to understand what it means. When you negate or deny a false statement your denial is correct, and when you negate or deny a true statement, you are wrong. Your denial is incorrect.

It probably seems obvious, but we could symbolize things roughly as follows;

¬ A false statement = a true statement
¬ A true statement = a false statement
Denying a false statement makes a true statement.
Denying a true statement makes a false statement.
Or
If you deny a false statement, you are telling the truth.
If you deny a true statement, you are telling a falsehood.

Practical applications:

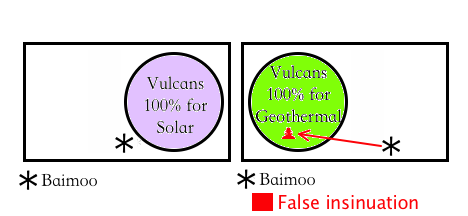
On the planet called Vulcan there are two sanctity groups, each about 5% of the population. They serve as priests, public welfare officers, and managers of the infrastructure. The violet robes believe Vulcan should use only solar power, no geo-thermal or other power. The green robes believe Vulcan should use only geo-thermal power and not solar power or anything else. When Baimoo competed for leadership of the violet robes during their half of the next cycle, it was noted that Baimoo had spoken in favor of experimental development of nuclear power. His great competitor among the violets said of him, "Baimoo is not a true advocate of solar power. Why would anyone support the candidacy for master of the violet robes of a Vulcan whose soul is green!"

Baimoo's opponent was, in effect, putting a "¬" symbol before the sentence "Baimoo is a true advocate of solar power." Was Baimoo's opponent being fair and truthful in his charge against him? What was Baimoo's opponent insinuating about him?